Navigation Slidewheel

As part of developing the sunwheel for correcting sextant height measurements, I also wanted to elmininate the need for the Pub249 almanacs that contain precomputed tables of the height $H_c$ and azimuth $Z_n$ for a celestial object as a function of the Latitude, Declination and Local Hour Angle.

(Note that the images on this page are from an older version of the navwheel and the newer one has dual log-cosine as well as expanded ranges)

For the $Z_n$ value I reinvented the universal astrolabe and added it to the back of the sun wheel since a 1 degree accuracy is sufficient. But the height calculation needs to be much more exact, within a few minutes, to be useful, so the estimate that the sun wheel gives for height was not adaquate.

Other folks have designed "emergency navigation" methods or made flattened versions of the Bygrave slide rule, although, since I'm full of hburis, I think mine has several advantages...

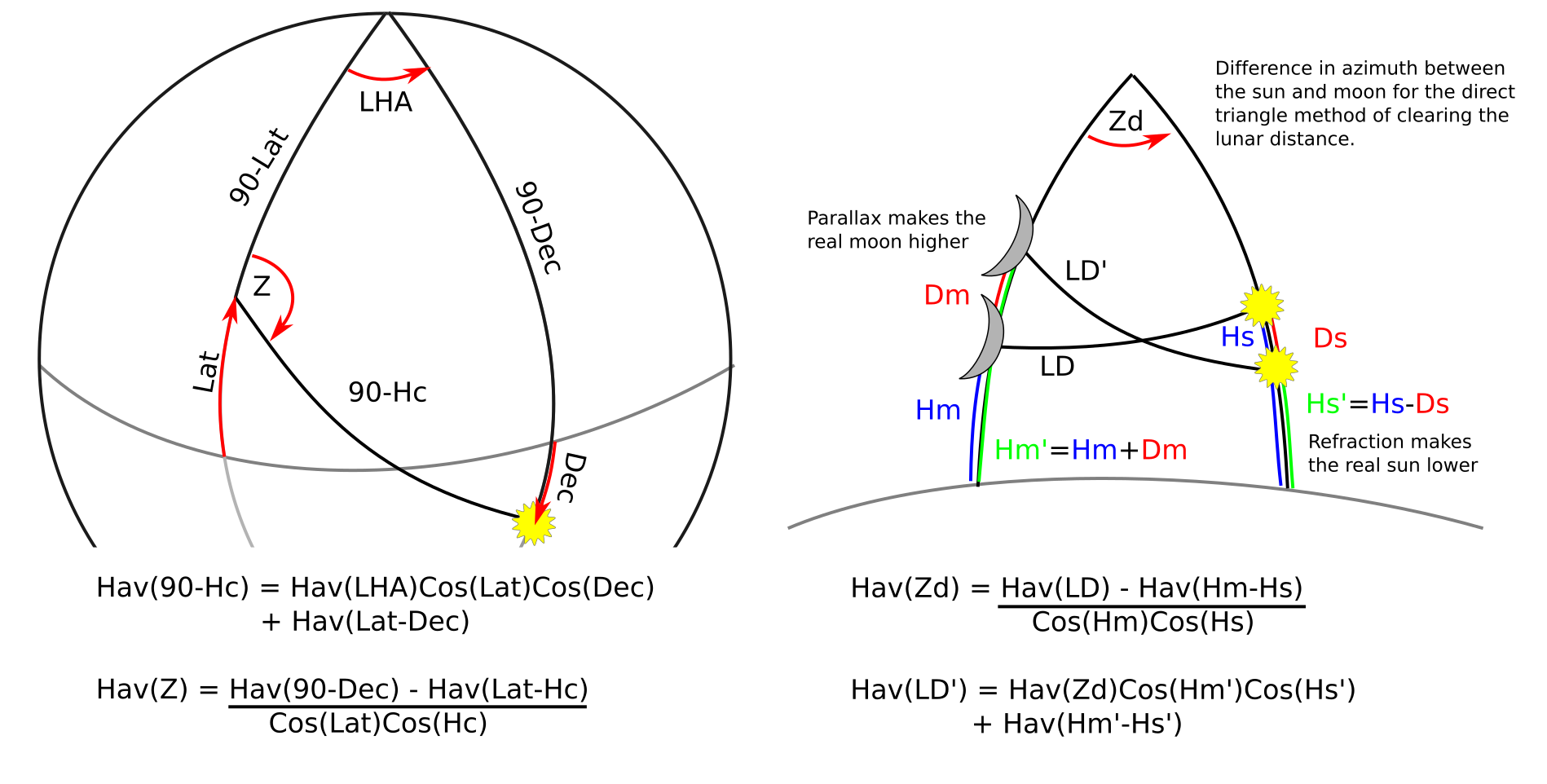
The three operations that are easily done with the navwheel are 1) computing the height $H_c$ of a celestial body given the declination of the star, the viewers assumed latitude, and the local hour angle between them, 2) using the computed height to compute the azimuth $Z$ from the assumed latitude to the star, and 3) clearing the lunar distance by the direct triangle method to correct for parallax and refraction that distorts the observed lunar distance.

Computing Height

Operation

To compute $H_c$ given the assumed Latitude, Local Hour Angle (LHA), and the Declination of the sun or star, start on the LHA side:

1. Rotate the inner wheel to align the red declination with the outer index
2. Align the pointer to the inner index (red declination 0)
3. Rotate the inner wheel to align the LHA with the pointer
4. Rotate the pointer clockwise to the latitude on the outer scale (passing the index once if the declination is also very high)
5. If the pointer crossed the inner index, move inwards one scale on the spiral
6. Read the transfer angle from the correct scale of the spiral

Flip to the Height side:

1. Align the pointer to the outer index
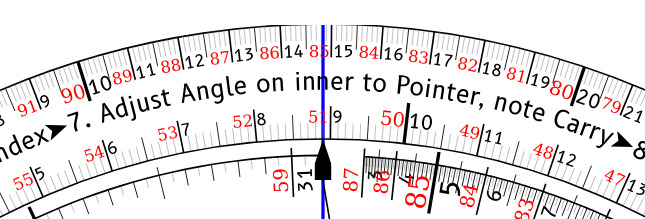
2. Rotate the inner wheel to align the transfer angle with the pointer. Make note of the carry value.
3. Align the pointer to the inner index
4. Rotate the inner wheel to align the Latitude - Declination with the pointer (or Declination - Latitude if that is easier)
5. Rotate the pointer clockwise to the outer index
6. If the pointer crossed the inner index, move inwards one scale on the spiral
7. Move inwards on the spiral based on the carry value
8. Read the $H_c$ value from the red numbers on the correct scale of the spiral.

With practice this is very fast and since you don't have to interpolate between the whole degree values as you do when using Pub249, I find it is significantly faster.

Example

As a worked example, let's say our DR latitude is 54°, the sun's declination is -11.25°, and Our observation is at a Local Hour Angle of 50.3° (before or after meridian; it doesn't matter).

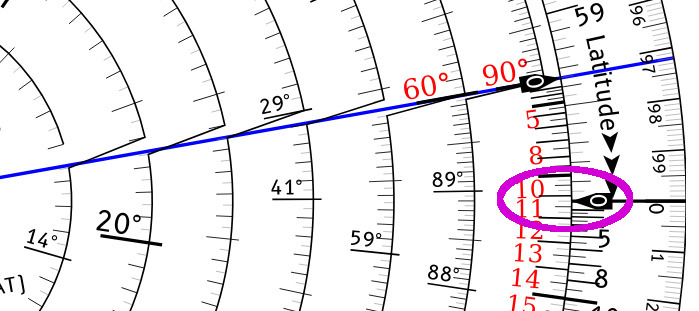
On the LHA side, set the Declination to 11.25° by lining it up with the zero (called the "Index") on the outer scale. Note that the sign for the declination does not matter -- north or south both use the same value. Then rotate the pointer so that it holds this position, relative to the outer scale.

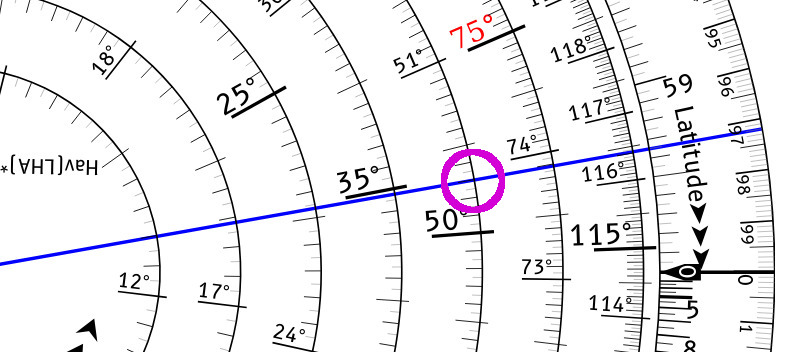
Next rotate the inner wheel so that the LHA, 50.3° lines up under the pointer.

Now rotate the pointer clockwise so that it lines up with the Latitude, 54° on the outer scale.

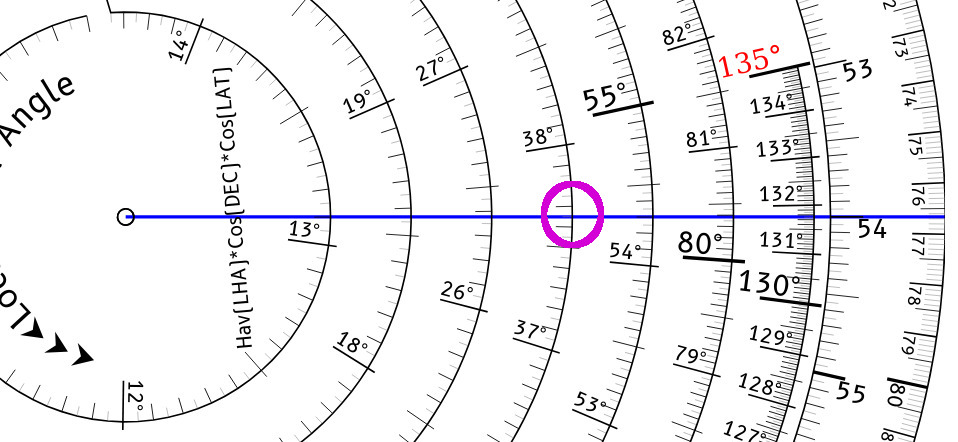
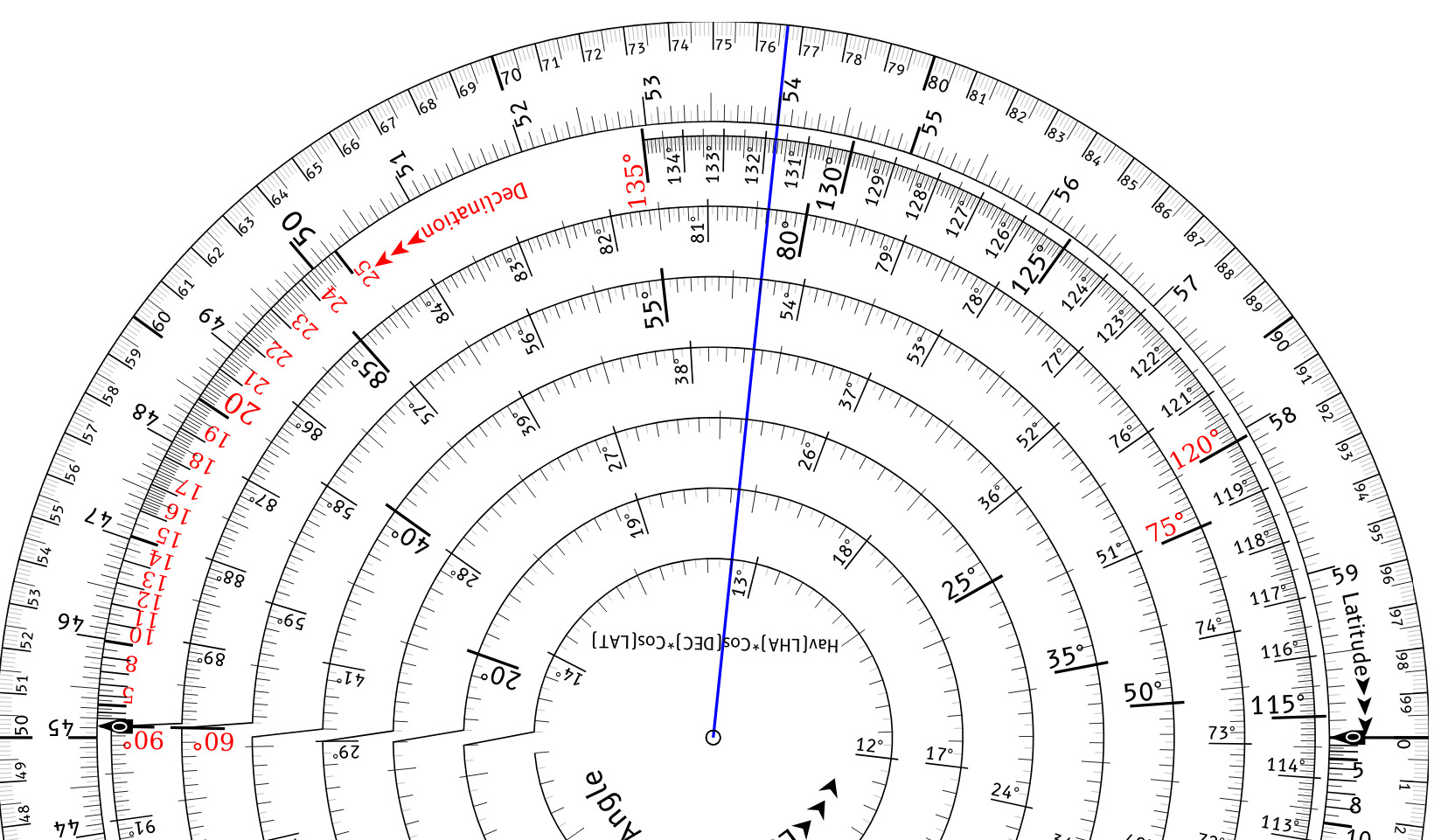
Since the pointer crossed the inner index, move to the next spiral inwards. The pointer is now indicating the Transfer Angle of 37.65° It is usually more comfortable to turn the entire wheel in your hands so that the pointer is level and you can easily read the numbers underneath it.

---

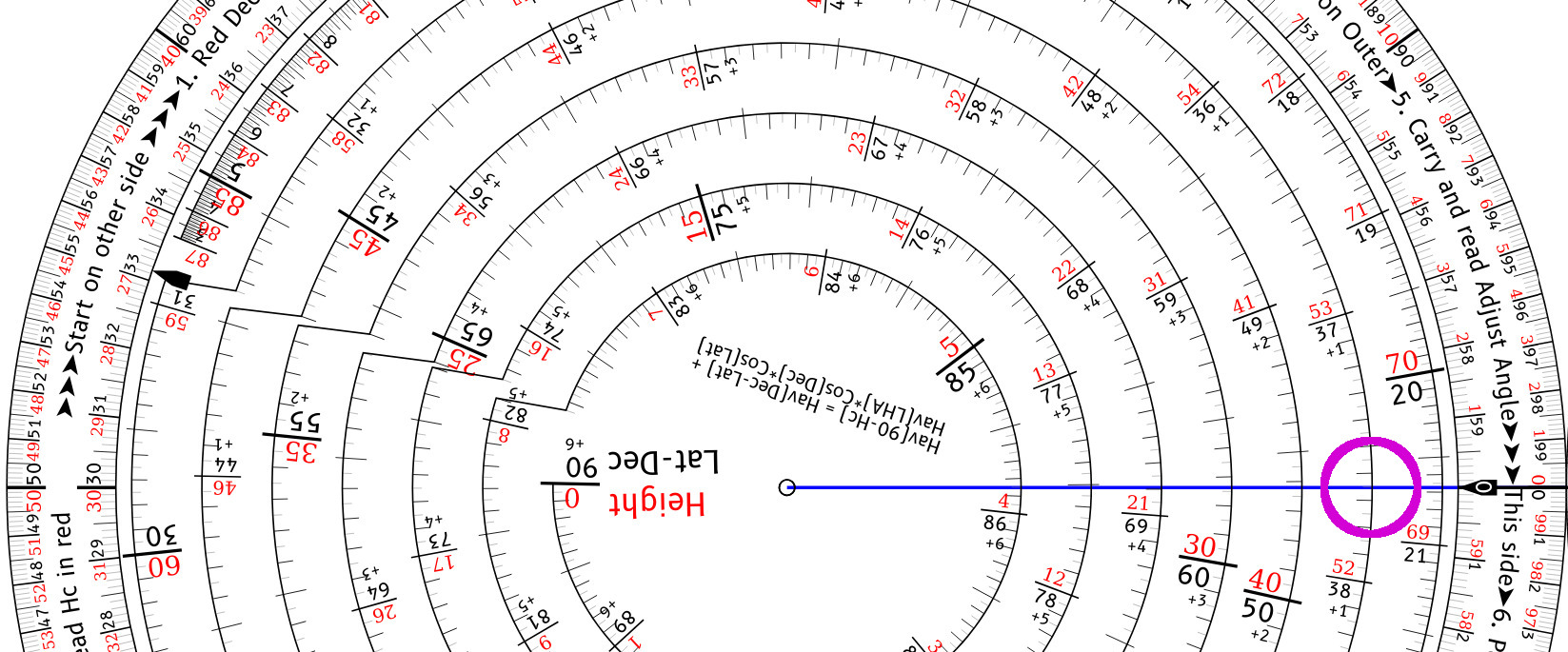
Flip the nav wheel to the Height side and align the pointer to the outer index, and use it to select the Transfer Angle 37.65° on the black digits of the inner spiral. Note that this spiral goes the other way from the LHA spiral, so the desired value is more clockwise than the digit. Make note of the Carry value of 1 for this Transfer Angle.

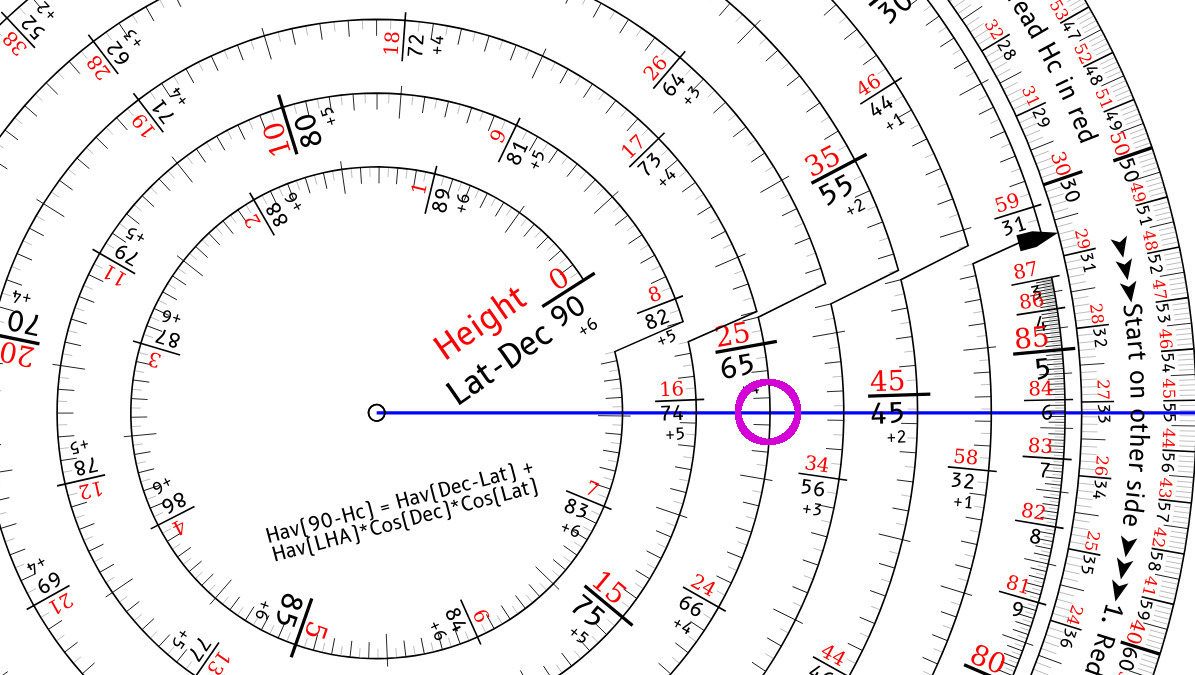
Move the pointer to the inner index, and then rotate the inner wheel to select the Latitude minus the Declination, $54 - -11.25$ = 65.25° We've rotate the wheel back again so that the pointer is horizontal to make it easier to read.

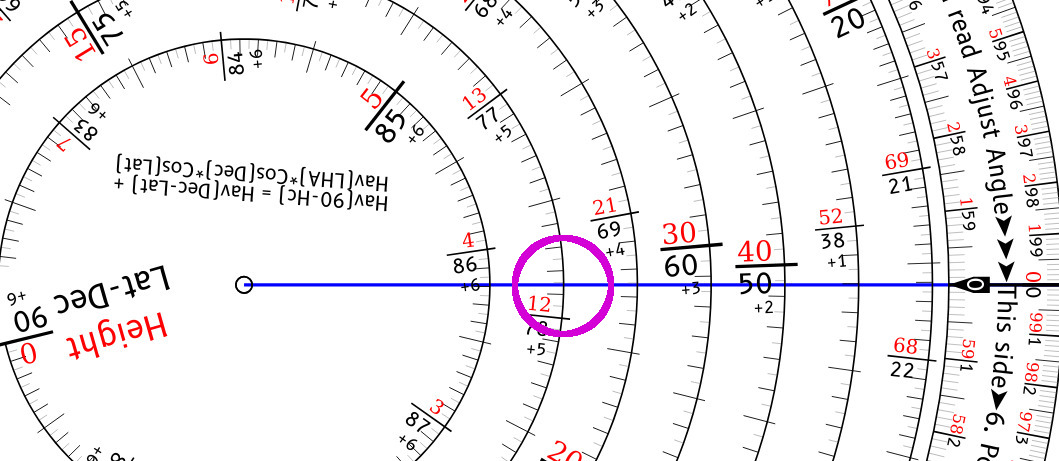
Finally rotate the pointer clockwise to the outer index, making note if we cross the inner index (in this case we don't). We move 1 step inwards on the spiral since there is a Carry from the Adjust angle, allowing us to read the $H_c$ in red as slightly less than 12.15° so perhaps 12.148°

The actual value from the formula is 12.1465°, so this is quite close!

If you want to convert the decimal degree to minutes, you can use the outer wheel on this side to select 14.8 and read 8.9', so the final result would be 12° 8.9'. Note that this outer scale does not have any connection to the inner Havesine scale and is only for performing this conversion (as well as having a visual guide to ensure that the pointer doesn't spin when you rotate the inner).

---

Computing Longitude

Operation

To compute the longitude given the known Latitude, Gloabl Hour Angle plus Declination of the sun or star, and the corrected observed height $H_o$, start on the Height side to perform the reverse operations.

1. First compute the absolute value of the difference between the Latitude and Declination (the sign does not matter).
2. Align the two indices
3. Set the pointer on the inner wheel to the Lat - Dec value in black, making note of the carry
4. Set the inner wheel to the $H_o$ value in red
5. Move the pointer counter clockwise to the outer index (to perform a subtraction)
6. If you cross the inner index, move outward one.
7. Move outward based on the carry,
8. Read the transfer angle in black from the inner.

Flip to the LHA side.

1. Set the pointer on the known Latitude on the outer ring
2. Move the inner wheel to align the index with the pointer
3. Move the the pointer to the Declination on the inner ring
4. Move the inner to align the Transfer Angle with the pointer
5. Rotate the pointer counter clockwise to the outer index.
6. If you cross the inner index, move outward one.
7. Read the Local Hour Angle from the spiral.
8. Since LHA + Longitude = GHA, Longitude is $GHA \pm LHA$. If the sight was before local noon, LHA is negative. If the sight was after local noon, LHA is positive. Remember that GHA is positive Eastward, while Longitude is positive West.

The Math

The function that we need to compute is

$$hav(90 - H_c) = hav(LHA) * \cos(Dec) * \cos(Lat) + hav(Lat - Dec)$$

Note that Haversine is symmetric around 0, so LHA can be positive or negative (before or after the meridian passage), and that the last term can be Latitude minus the Declination or Declination minus Latitude, only the absolute value matters.

Another thing to note is that if LHA is 0 or very small, which means the sight is near the meridian passage, then the first term goes to almost zero, so the result is going to be very close to the the simplified $H_c = 90 - (Lat - Dec)$

LHA side

The spiral on the first side of the slide rule computes $\log(hav(LHA)$ and the outer markings compute $\log(\cos(Lat))$ and $\log(\cos(Dec))$. Since adding logarithms performs multiplication, this allows us to compute the log of the transfer angle:

$$\begin{align} \alpha & = \log(hav(LHA)) + \log(\cos(Dec)) + \log(\cos(Lat)) \\ & = \log(hav(LHA) \cos(Dec) \cos(Lat)) \end{align}$$

By "backing up" an amount equal to $\log(\cos(Dec))$ and then going forward to an amount equal to $\log(\cos(Lat))$, the rule efficiently computes the product. Adding that to the the $\log(hav(LHA))$ value multiplies that as well, producing the intermediate product that we require.

The outer scale is $\log(\cos(60\deg))$ radians since that is the maximum longitude that is supported, and which means that each wrap of the spiral is of the same length. It starts to get very spread out at smaller angles, so a cutoff of 10° was chosen for practical purposes. LHA less than that means the sun is almost directly overhead and you're within a few minutes of the merdian passage, so just do a normal latitude calculation instead.

And by then reading the value from the spiral, it computes:

$$\begin{align} A & = hav^{-1}(e^\alpha) \\ & = hav^{-1}(e^{\log(hav(LHA) \cos(Dec) \cos(Lat))}) \\ & = hav^{-1}(hav(LHA) \cos(Dec) \cos(Lat)) \end{align}$$

This value is recorded and then transfered to the Height side.

Height side

This spiral computes $hav(A)$ without the logarithm, so adding values on it is normal addition. The transfer angle from the LHA side is $hav(hav^{-1}(A))) = A$, when we set the pointer to $A$ this results in the partial value $hav(LHA) \cos(Dec) \cos(Lat)$ on the outer ring (plus a carry value that indicates how many loops on this spiral have been traversed).

By adding the length of the transfer angle to the length of $hav(Lat-Dec)$ and by inwards by the number of carries, this results in the sum $hav(Lat-Dec) + hav(LHA)\cos(Dec)\cos(Lat)$, modulo the number of turn. Add the carry value to move inward by that many turns and now the inverse Haversine can be applied to read the $H_c$ value from the red numbers along the spiral (since the red values are ninety minus the black).

Computing Bearing

Once the $H_c$ has been computed, it is also necessary to compute the bearing to the sun or star for plotting using the intercept method. This could be done on on the astrolabe, but it can also be done more accurately with the navwhele.

The math is similar:

$$\begin{align} hav(90 - Dec) &= hav(Z) \cos(H_c) \cos(Lat) + hav(Lat - H_c) \\ hav(Z) \cos(H_c) \cos(Lat) &= hav(90 - Dec) - hav(Lat - H_c) \\ hav(Z) &= { hav(90 - Dec) - hav(Lat - H_c) \over \cos(H_c) \cos(Lat) } \end{align}$$

Start on the linear side with $90-Dec$ on the spiral, which can be read directly from the red numbers. Note that if the sun is in the southern hemisphere and $Dec$ is negative, then use the negative red values.

When the final result is read from the log scale, northern hemisphere readings use the red values for $360-Z$ while southern hemisphere can use the black values.

Computing Longitude

The math is the reverse operation of compute $H_c$:

$$\begin{align} hav(90 - H_o) &= hav(LHA)\cos(Dec)\cos(Lat) + hav(Lat - Dec) \\ hav(LHA) \cos(Dec)\cos(Lat) &= hav(90 - H_o) - hav(Lat-Dec) \\ hav(LHA) &= {hav(90 - H_o) - hav(Lat-Dec) \over \cos(Dec)\cos(Lat)} \\ \end{align}$$

The division is done with logarithms the same way as the multiplication, which is why the pointer moves counter clockwise since it is subtracting

Source Code

• github.com/osresearch/sunwheel make-haversine.py
• https://raw.githubusercontent.com/osresearch/sunwheel/refs/heads/main/haversine.svg

2026 Sailing