Universal Astrolabe

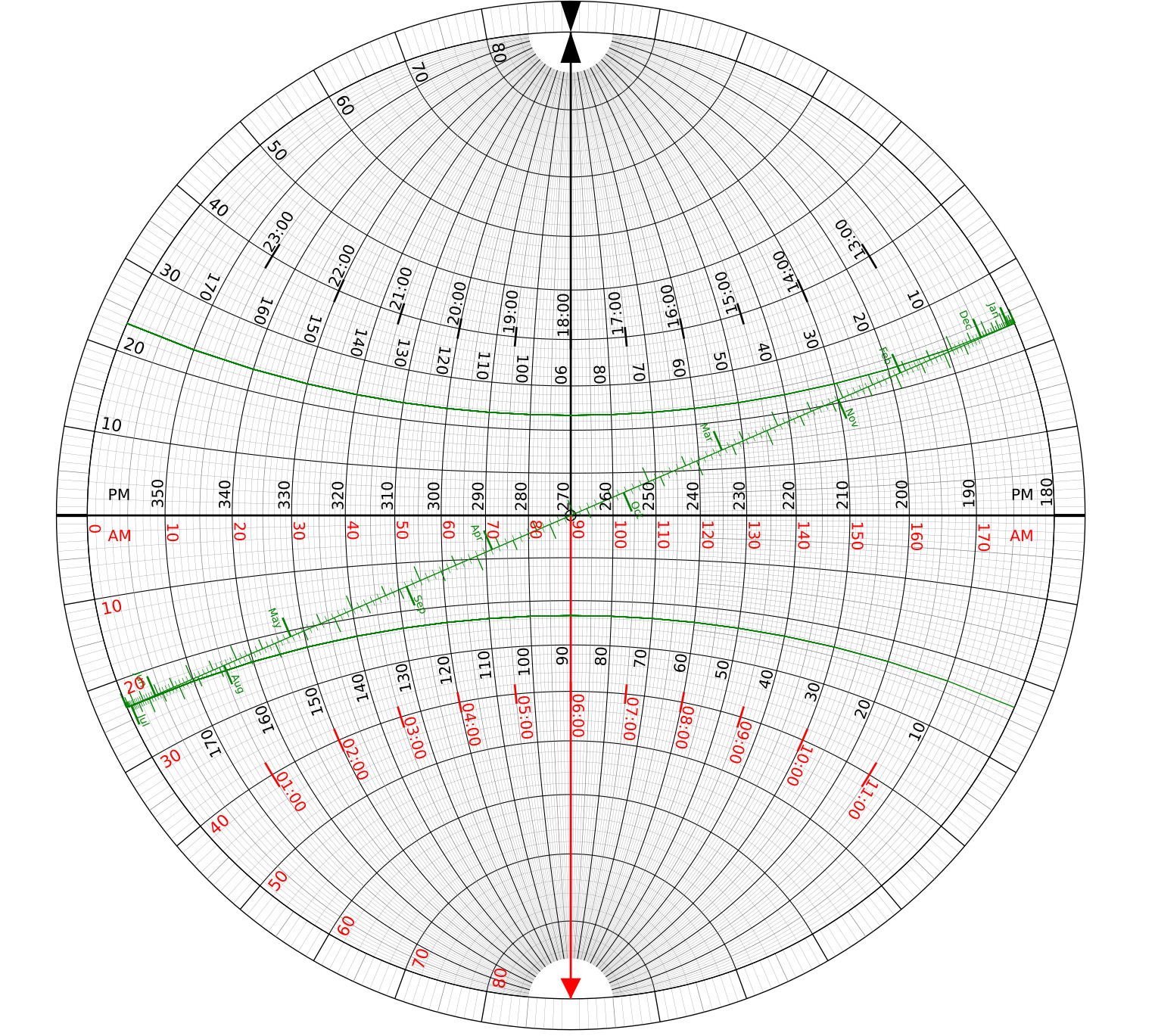
Universal astrolabe image

As a companion to the navwheel that computes the height of a celestial object, you also need the azimuth or bearing to it. These are pre-computed for different latitudes, declinations and local hour angles in Pub249 almanacs, but those are some big books to carry around.

Operation

This is easiest on the slidewheel version, but can also be done with a printed sheet and a piece of plastic. Using the slide rule you can point at the desired parameters, while on the plastic sheet you must mark the center of the disc with a small dot and the north pole with a line, then mark a small dot for the hour angle and declination of the Sun at the time of your observation.

Note that all the way to the right on the diagram is a local hour angle of zero, which corresponds to local noon.

Rotate the slide rule inner face clockwise so that the outer index lines up with your with your latitude. If you're using the sheet, rotate it counter clockwise so that the north pole line lines up with your approximate latitude and the center dot stays in the center. If you are in the Southern Hemisphere, keep rotating the inner wheel or sheet until the pole lines up with the red latitude below the horizontal equator.

Now follow the vertical line from the dot that you marked for the sun to the horizontal line. If your observation is before the meridian (AM), then read the red bearing. If your observation is after local noon (PM), then read the black bearing.

The approximate height of the sun can also be read from the same scale as the latitude.

Example

Stat	Value
Latitude	+19°
LHA	11°
Declination	-15°

The LHA of 11° and Sun's declination of -15° are marked on the sheet. This hour angle could correspond to either 11:15 or 12:45.

The slide rule wheel has been rotated counter clockwise until the outer index intersects the 19° latitude on the left side. The dot for the sun has climbed to around 54° of height and if you follow the vertical line to the equator it intersects around the 162° mark (for an AM observation) or 198° (for a PM).

There is no need to do additional math based on which hemisphere, if LHA is greater than 180 or "Same Name" / "Contrary Name".

If you're using a plastic sheet, here is what they would look like. Note that it is not as precise as the pointer on the slide rule, but close enough for most casual plotting.


Setup	Reading the bearing

Math

This is an accidental rediscovery of the universal astrolabe and takes advantage of the fact that rotating a vector by an angle has the effect of multiplying by a transform matrix such that the end result matches the desired function for the bearing computation. The stereographic projection takes two inputs $x,y$ and outputs $x',y'$ :

$\begin{bmatrix} x' \\ y' \end{bmatrix} = {1\over 1 + \cos(x)\cos(y)} \begin{bmatrix} \cos(x)\sin(y) \\ \sin(y) \end{bmatrix}$

The first projection takes the inputs of Declination and LHA (note that the center is LHA=90), and produces an XY coordinate of:

$\begin{align} \begin{bmatrix} X_1 \\ Y_1 \end{bmatrix} & = { 1 \over 1 + \cos(Dec) \cos(90-LHA) } \begin{bmatrix} \cos(Dec) \sin(90-LHA) \\ \sin(Dec) \end{bmatrix} \\ & = { 1 \over 1 + \cos(Dec) \sin(LHA) } \begin{bmatrix} \cos(Dec) \cos(LHA) \\ \sin(Dec) \end{bmatrix} \\ & = K_1 \begin{bmatrix} \cos(Dec) \cos(LHA) \\ \sin(Dec) \end{bmatrix} \end{align}$

Rotating the sheet counter clockwise by $90 - Lat$ multiplies $(X_1,Y_1)$ by the rotation matrix:

$\begin{bmatrix} \cos(90-Lat)) & -\sin(90-Lat) \\ \sin(90-Lat) & \cos(90-Lat) \end{bmatrix} \begin{bmatrix} X_1 \\ Y_1 \end{bmatrix} = \begin{bmatrix} \sin(Lat) & -\cos(Lat) \\ \cos(Lat) & \sin(Lat) \end{bmatrix} \begin{bmatrix} X_1 \\ Y_1 \end{bmatrix}$

Which expands to:

$\begin{bmatrix} X_2 \\ Y_2 \end{bmatrix} = K_1 \begin{bmatrix} \sin(Lat)\cos(Dec)\cos(LHA) - \cos(Lat)\sin(Dec) \\ \cos(Lat)\cos(Dec)\cos(LHA) + \sin(Lat)\sin(Dec) \end{bmatrix}$

Working the other way, if we project $H_c$ and $Z$ (where 0 is all the way to the left side) we get

$\begin{align} \begin{bmatrix} X_3 \\ Y_3 \end{bmatrix} & = { 1 \over 1 + \cos(H_c)\cos(Z+90) } \begin{bmatrix} \cos(H_c) \sin(Z+90) \\ \sin(H_c) \end{bmatrix} \\ & = { 1 \over 1 - \cos(H_c)\sin(Z) } \begin{bmatrix} \cos(H_c) \cos(Z) \\ \sin(H_c) \end{bmatrix} \\ & = K_2 \begin{bmatrix} \cos(H_c) \sin(Z) \\ \sin(H_c) \end{bmatrix} \end{align}$

However, we can fill in the formulas for $H_c$ and $Z$ and the spherical triangle formula:

$\sin(H_c) = \sin(Dec)\sin(Lat) + \cos(Lat)\cos(Dec)\cos(LHA)$

$\cos(Z) = {\sin(Dec) - \sin(Lat)\sin(H_c) \over \cos(Lat)\cos(H_c)}$

${\sin(Z)\over \cos(Decl)} = {\sin(LHA)\over \cos(H_c)} = {\sin(W)\over \cos(Lat)}$

First we need to show that $K_1 = K_2$ .

$\require{cancel} \begin{align} {1\over K_1} = 1 - \cos(Dec)\sin(LHA) & \stackrel{?}{=} 1 - \cos(H_c)\sin(Z) = {1\over K_2} \\ \cos(Dec)\sin(LHA) & \stackrel{?}{=} \cos(H_c)\sin(Z) \\ \cos(Dec)\sin(LHA) & \stackrel{?}{=} \cos(H_c)\sin(Z) \\ \cancel{\cos(Dec)}{\cos(H_c)\sin(Z)\over\cancel{\cos(Dec)}} & \stackrel{?}{=} \cos(H_c)\sin(Z) \\ \cos(H_c)\sin(Z) & = \cos(H_c)\sin(Z) \\ K_1 & \stackrel{\therefore}{=} K_2 \end{align}$

Then we can note that the rotated value for $Y_2$ is the same as $\sin(H_c)$ :

$\begin{align} Y_2 &= K_1 (\cos(Lat)\cos(Dec)\cos(LHA) + \sin(Lat)\sin(Dec)) \\ &= K_2 \sin(H_c) \\ &= Y_3 \end{align}$

And lastly that $X_2=X_3$ :

$\begin{align} X_3 &= \cos(H_c)\cos(Z) \\ &= \cancel{\cos(H_c)}{\sin(Dec)-\sin(Lat)\sin(H_c) \over \cos(Lat) \cancel{\cos(H_c)}} \\ &= {\sin(Dec) - \sin(Lat)(\sin(Dec)\sin(Lat) + \cos(Lat)\cos(Dec)\cos(LHA)) \over \cos(Lat)} \\ &= {\sin(Dec) - \sin^2(Lat)\sin(Dec) - \sin(Lat)\cos(Lat)\cos(Dec)\cos(LHA) \over \cos(Lat)} \\ &= {\sin(Dec)(1 - \sin^2(Lat)) - \sin(Lat)\cos(Lat)\cos(Dec)\cos(LHA) \over \cos(Lat) } \\ &= { \sin(Dec)\cos^2(Lat) - \sin(Lat)\cos(Lat)\cos(Dec)\cos(LHA) \over \cos(Lat) } \\ &= \cancel{\cos(Lat)}{ \sin(Dec)\cos(Lat) - \sin(Lat)cos(Dec)\cos(LHA) \over \cancel{\cos(Lat)} } \\ &= \sin(Dec)\cos(Lat) - \sin(Lat)\cos(Dec)\cos(LHA) \end{align}$

Which is actually $-X_2$ , so I must have made a sign error somewhere but the math mostly works out. Please send me an email if you see the error. I'm really bad at the details sometimes.

Source Code

2026 Sailing